잔글편집 요약 없음 |
잔글편집 요약 없음 |
||
| (같은 사용자의 중간 판 29개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
[[분류:용어]] | [[분류:용어]] | ||
<big>Standing Wave Ratio (SWR)</big> | <big>'''Standing Wave Ratio''' (SWR)</big> | ||
==개요== | ==개요== | ||
정재파비(SWR) 또는 전압정재파비(VSWR)는 교류 회로에서 | 정재파비(SWR) 또는 전압정재파비(VSWR)는 교류 회로에서 반사파로 인한 신호 손실 정도를 나타낸다. 정재파비는 1에 가깝게 낮을수록 신호가 온전하게 통과하는 것이고 무한대에 가까울수록 신호가 덜 통과하는 것이다. | ||
===반사파=== | |||
서로 접속한 도체 사이에 [[임피던스]] 차이가 존재하면 교류 전류가 온전히 통과하지 못하면서 반사파가 발생한다. | |||
반사파가 지나치게 발생하면 안테나에서 제대로 방사되지 않고 되돌아오는 전류가 송수신부에 무리를 주게 된다. | |||
극단적인 예시를 들자면 무전기에 안테나를 연결하지 않거나 급전선아 끊겨있을 경우, 임피던스가 50Ω인 무전기가 무한대 임피던스에 접속된 것과 마찬가지이므로, 송신부가 출력한 전류가 그대로 송신부로 되돌아온다. | |||
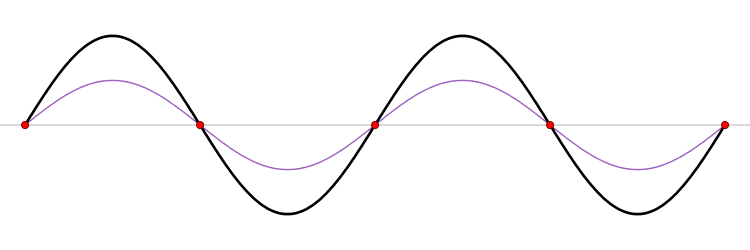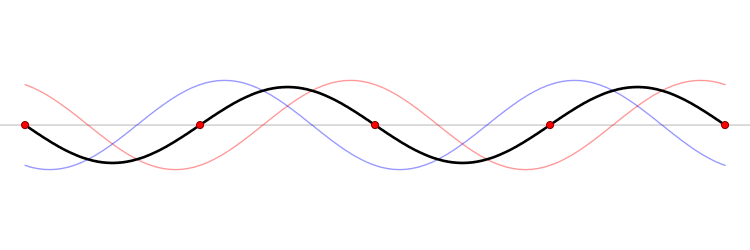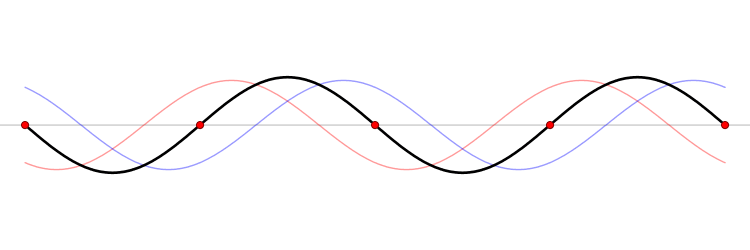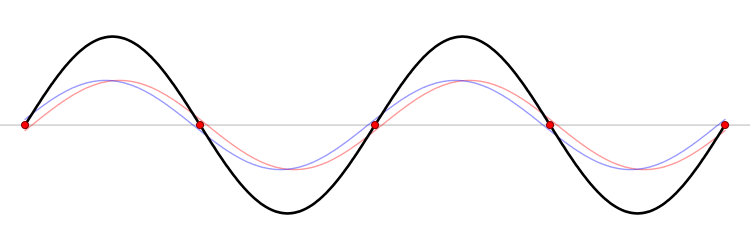
===정재파=== | ===정재파=== | ||
[[파일:standing_wave.gif]] | [[파일:standing_wave.gif]] | ||
정재파는 임피던스 차이에 의해 반사파가 | 정재파는 임피던스 차이에 의해 발생한 반사파가 본래 신호파와 합성되어 만들어진 파형을 뜻한다. 정재파(Standing Wave)라 불리는 이유는 두 파형이 합성될 때 제자리에서 진동하는 듯한 파형을 보이기 때문이다. | ||
===정재파비의 개선=== | ===정재파비의 개선=== | ||
* 정재파비를 개선하기 위해서는 반사파를 줄여 정재파를 최소화해야 한다. | * 정재파비를 개선하기 위해서는 반사파를 줄여 정재파를 최소화해야 한다. | ||
* 송신 선로를 송신기의 임피던스(보통 50Ω)에 맞추어야 하는데 커넥터와 케이블은 정격 임피던스 제품을 사용해야 하고, | * 송신 선로를 송신기의 임피던스(보통 50Ω)에 맞추어야 하는데 커넥터와 케이블은 정격 임피던스 제품을 사용해야 하고, 안테나의 급전점 임피던스와 차이가 있을 경우 임피던스를 정합하기 위한 [[튜너]]가 필요하다. | ||
* [[안테나]]를 실내에서 운용하거나 안테나 | * [[안테나]]를 실내에서 운용하거나 안테나 가까이에 장애물이 있어도 방사된 전파가 일부 반사되어 안테나로 되돌아와 송신 회로에 반사파가 발생하고 정재파비가 높아지므로 유의한다. | ||
==계산== | ==계산== | ||
===반사 계수=== | ===반사 계수=== | ||
우선 반사 계수(Reflection Coefficient)에 대해 알 필요가 있다.<br /> | |||
반사 | 반사 계수는 반사파가 발생하는 정도를 계수로 나타낸 것이다. 기호는 <math>\mathrm{L}</math>을 상하로 반전시켜 <math>\Gamma</math>(대문자 감마)로 나타내며, 다음과 같이 입사파(<math>V_\mathrm{I}</math>) 대비 반사파(<math>V_\mathrm{R}</math>)의 전압비로 나타내고 0에 가까울수록 좋다. | ||
<math>\Gamma=\frac{V_\mathrm{R}}{V_\mathrm{I}}</math> | <math>\Gamma=\frac{V_\mathrm{R}}{V_\mathrm{I}}</math> | ||
다음과 같이 특성 임피던스(<math>Z_\mathrm{0}</math>)와 종단 부하 임피던스(<math>Z_\mathrm{L}</math>)로도 나타낼 수 있다. | |||
<math>\Gamma=\frac{Z_\mathrm{L}-Z_\mathrm{0}}{Z_\mathrm{L}+Z_\mathrm{0}}</math> | |||
역방향으로 반사되는 것을 생각하면 반사파의 전압은 음의 값을 가지므로 반사 계수는 음수가 되나, 절댓값의 형태를 주로 활용한다.<br /> | |||
[[S-파라미터]]에서는 <math>S_{11}</math> 또는 <math>S_{22}</math>로 나타낸다. | |||
한편, 반사 계수를 이용하여 투과 계수를 나타낼 수도 있다. | |||
=== | <math>\tau=\frac{V_\mathrm{T}}{V_\mathrm{I}}=\frac{V_\mathrm{I}+V_\mathrm{R}}{V_\mathrm{I}}=1+\Gamma</math> | ||
===정재파비=== | ===정재파비=== | ||
정재파비는 반사 계수의 | 정재파비는 반사 계수의 절댓값을 이용해 다음과 같이 입사파에서 반사파를 제외한(간단히 말해 투과하는) 파형 대비 정재파의 진폭비로 나타내진다. | ||
<math>\mathrm{SWR}=\frac{1+|\Gamma|}{1-|\Gamma|}</math> | <math>\mathrm{SWR}=\frac{1+|\Gamma|}{1-|\Gamma|}</math> | ||
정재파비는 항상 1 이상이 되고 1에 가깝게 | 정재파비는 항상 1 이상이 되고 1에 가깝게 낮을수록 좋으며, 반사파가 존재하지 않는 경우는 현실적으로 불가능하기 때문에 정수 <math>1</math>보다는 항상 크다. | ||
===반사 손실=== | |||
반사 계수를 이용해 반사 손실(Return Loss)의 비율을 [[dB|dB(데시벨)]]로 나타낼 수 있다. '반사파가 손실되는 정도', 즉 투과하는 정도를 의미하는 것이므로 유의한다. 반사 계수의 역수를 사용해 반사파 <math>V_\mathrm{R}</math> 대비 입사파 <math>V_\mathrm{I}</math>의 전압비로 나타내므로 높을수록 좋으며, RMS 속성이기 때문에 dB 계산에는 제곱한 값을 이용한다. | |||
<math>\mathrm{L}_\mathrm{R}=10\log_{10}\left|\frac{V_\mathrm{I}}{V_\mathrm{R}}\right|^2=10\log_{10}\frac{1}{|\Gamma|^2}</math><br /> <math>=-20\log_{10}\left|\frac{V_\mathrm{R}}{V_\mathrm{I}}\right|=-20\log_{10}|\Gamma|</math> | |||
==환산표== | ==환산표== | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ | ||
!<math>\mathrm{SWR}</math> | !정재파비<br /><math>\mathrm{SWR}</math> | ||
!<math>|\Gamma|</math> | !반사 계수<br /><math>|\Gamma|</math> | ||
!반사 손실<br />(dB) | !반사 손실<br /><math>\mathrm{L_R(dB)}</math> | ||
! | !투과 손실<br /><math>\mathrm{L_T(\%)}</math> | ||
|- | |- | ||
|style="text-align: center;"|1.00 | |style="text-align: center;"|1.00 | ||
| 97번째 줄: | 110번째 줄: | ||
!<math>\mathrm{SWR}</math> | !<math>\mathrm{SWR}</math> | ||
!<math>|\Gamma|</math> | !<math>|\Gamma|</math> | ||
! | !<math>\mathrm{L_R(dB)}</math> | ||
! | !<math>\mathrm{L_T(\%)}</math> | ||
|- | |- | ||
|style="text-align: center;"|1.60 | |style="text-align: center;"|1.60 | ||
| 152번째 줄: | 165번째 줄: | ||
!<math>\mathrm{SWR}</math> | !<math>\mathrm{SWR}</math> | ||
!<math>|\Gamma|</math> | !<math>|\Gamma|</math> | ||
! | !<math>\mathrm{L_R(dB)}</math> | ||
! | !<math>\mathrm{L_T(\%)}</math> | ||
|- | |- | ||
|style="text-align: center;"|3.00 | |style="text-align: center;"|3.00 | ||
2022년 5월 12일 (목) 22:49 기준 최신판
Standing Wave Ratio (SWR)
개요
정재파비(SWR) 또는 전압정재파비(VSWR)는 교류 회로에서 반사파로 인한 신호 손실 정도를 나타낸다. 정재파비는 1에 가깝게 낮을수록 신호가 온전하게 통과하는 것이고 무한대에 가까울수록 신호가 덜 통과하는 것이다.
반사파
서로 접속한 도체 사이에 임피던스 차이가 존재하면 교류 전류가 온전히 통과하지 못하면서 반사파가 발생한다.
반사파가 지나치게 발생하면 안테나에서 제대로 방사되지 않고 되돌아오는 전류가 송수신부에 무리를 주게 된다.
극단적인 예시를 들자면 무전기에 안테나를 연결하지 않거나 급전선아 끊겨있을 경우, 임피던스가 50Ω인 무전기가 무한대 임피던스에 접속된 것과 마찬가지이므로, 송신부가 출력한 전류가 그대로 송신부로 되돌아온다.
정재파
정재파는 임피던스 차이에 의해 발생한 반사파가 본래 신호파와 합성되어 만들어진 파형을 뜻한다. 정재파(Standing Wave)라 불리는 이유는 두 파형이 합성될 때 제자리에서 진동하는 듯한 파형을 보이기 때문이다.
정재파비의 개선
- 정재파비를 개선하기 위해서는 반사파를 줄여 정재파를 최소화해야 한다.
- 송신 선로를 송신기의 임피던스(보통 50Ω)에 맞추어야 하는데 커넥터와 케이블은 정격 임피던스 제품을 사용해야 하고, 안테나의 급전점 임피던스와 차이가 있을 경우 임피던스를 정합하기 위한 튜너가 필요하다.
- 안테나를 실내에서 운용하거나 안테나 가까이에 장애물이 있어도 방사된 전파가 일부 반사되어 안테나로 되돌아와 송신 회로에 반사파가 발생하고 정재파비가 높아지므로 유의한다.
계산
반사 계수
우선 반사 계수(Reflection Coefficient)에 대해 알 필요가 있다.
반사 계수는 반사파가 발생하는 정도를 계수로 나타낸 것이다. 기호는 [math]\displaystyle{ \mathrm{L} }[/math]을 상하로 반전시켜 [math]\displaystyle{ \Gamma }[/math](대문자 감마)로 나타내며, 다음과 같이 입사파([math]\displaystyle{ V_\mathrm{I} }[/math]) 대비 반사파([math]\displaystyle{ V_\mathrm{R} }[/math])의 전압비로 나타내고 0에 가까울수록 좋다.
[math]\displaystyle{ \Gamma=\frac{V_\mathrm{R}}{V_\mathrm{I}} }[/math]
다음과 같이 특성 임피던스([math]\displaystyle{ Z_\mathrm{0} }[/math])와 종단 부하 임피던스([math]\displaystyle{ Z_\mathrm{L} }[/math])로도 나타낼 수 있다.
[math]\displaystyle{ \Gamma=\frac{Z_\mathrm{L}-Z_\mathrm{0}}{Z_\mathrm{L}+Z_\mathrm{0}} }[/math]
역방향으로 반사되는 것을 생각하면 반사파의 전압은 음의 값을 가지므로 반사 계수는 음수가 되나, 절댓값의 형태를 주로 활용한다.
S-파라미터에서는 [math]\displaystyle{ S_{11} }[/math] 또는 [math]\displaystyle{ S_{22} }[/math]로 나타낸다.
한편, 반사 계수를 이용하여 투과 계수를 나타낼 수도 있다.
[math]\displaystyle{ \tau=\frac{V_\mathrm{T}}{V_\mathrm{I}}=\frac{V_\mathrm{I}+V_\mathrm{R}}{V_\mathrm{I}}=1+\Gamma }[/math]
정재파비
정재파비는 반사 계수의 절댓값을 이용해 다음과 같이 입사파에서 반사파를 제외한(간단히 말해 투과하는) 파형 대비 정재파의 진폭비로 나타내진다.
[math]\displaystyle{ \mathrm{SWR}=\frac{1+|\Gamma|}{1-|\Gamma|} }[/math]
정재파비는 항상 1 이상이 되고 1에 가깝게 낮을수록 좋으며, 반사파가 존재하지 않는 경우는 현실적으로 불가능하기 때문에 정수 [math]\displaystyle{ 1 }[/math]보다는 항상 크다.
반사 손실
반사 계수를 이용해 반사 손실(Return Loss)의 비율을 dB(데시벨)로 나타낼 수 있다. '반사파가 손실되는 정도', 즉 투과하는 정도를 의미하는 것이므로 유의한다. 반사 계수의 역수를 사용해 반사파 [math]\displaystyle{ V_\mathrm{R} }[/math] 대비 입사파 [math]\displaystyle{ V_\mathrm{I} }[/math]의 전압비로 나타내므로 높을수록 좋으며, RMS 속성이기 때문에 dB 계산에는 제곱한 값을 이용한다.
[math]\displaystyle{ \mathrm{L}_\mathrm{R}=10\log_{10}\left|\frac{V_\mathrm{I}}{V_\mathrm{R}}\right|^2=10\log_{10}\frac{1}{|\Gamma|^2} }[/math]
[math]\displaystyle{ =-20\log_{10}\left|\frac{V_\mathrm{R}}{V_\mathrm{I}}\right|=-20\log_{10}|\Gamma| }[/math]
환산표
| 정재파비 [math]\displaystyle{ \mathrm{SWR} }[/math] |
반사 계수 [math]\displaystyle{ |\Gamma| }[/math] |
반사 손실 [math]\displaystyle{ \mathrm{L_R(dB)} }[/math] |
투과 손실 [math]\displaystyle{ \mathrm{L_T(\%)} }[/math] |
|---|---|---|---|
| 1.00 | 0.00 | [math]\displaystyle{ \infty }[/math] | 0.00
|
| 1.05 | 0.02 | 32.26 | 0.06
|
| 1.10 | 0.05 | 26.44 | 0.23
|
| 1.15 | 0.07 | 23.13 | 0.49
|
| 1.20 | 0.09 | 20.83 | 0.83
|
| 1.25 | 0.11 | 19.09 | 1.23
|
| 1.30 | 0.13 | 17.69 | 1.70
|
| 1.35 | 0.15 | 16.54 | 2.22
|
| 1.40 | 0.17 | 15.56 | 2.78
|
| 1.45 | 0.18 | 14.72 | 3.37
|
| 1.50 | 0.20 | 13.98 | 4.00 |
| [math]\displaystyle{ \mathrm{SWR} }[/math] | [math]\displaystyle{ |\Gamma| }[/math] | [math]\displaystyle{ \mathrm{L_R(dB)} }[/math] | [math]\displaystyle{ \mathrm{L_T(\%)} }[/math]
|
| 1.60 | 0.23 | 12.74 | 5.33
|
| 1.70 | 0.26 | 11.73 | 6.72
|
| 1.80 | 0.29 | 10.88 | 8.16
|
| 1.90 | 0.31 | 10.16 | 9.63
|
| 2.00 | 0.33 | 9.54 | 11.11
|
| 2.10 | 0.35 | 9.00 | 12.60
|
| 2.20 | 0.38 | 8.52 | 14.06
|
| 2.30 | 0.39 | 8.09 | 15.52
|
| 2.40 | 0.41 | 7.71 | 16.96
|
| 2.50 | 0.43 | 7.36 | 18.36 |
| [math]\displaystyle{ \mathrm{SWR} }[/math] | [math]\displaystyle{ |\Gamma| }[/math] | [math]\displaystyle{ \mathrm{L_R(dB)} }[/math] | [math]\displaystyle{ \mathrm{L_T(\%)} }[/math]
|
| 3.00 | 0.50 | 6.02 | 25.00
|
| 3.50 | 0.56 | 5.11 | 30.86
|
| 4.00 | 0.60 | 4.44 | 36.00
|
| 4.50 | 0.64 | 3.93 | 40.50
|
| 5.00 | 0.67 | 3.52 | 44.45
|
| 6.00 | 0.71 | 2.92 | 51.01
|
| 7.00 | 0.75 | 2.50 | 56.25
|
| 8.00 | 0.78 | 2.18 | 60.50
|
| 9.00 | 0.80 | 1.94 | 64.00
|
| 10.00 | 0.81 | 1.74 | 66.39
|
| [math]\displaystyle{ \infty }[/math] | 1.00 | 0.00 | 100.00
|