(새 문서: 분류:전파공학 분류:전자기학분류:이론분류:전기와 자기 =====저항===== 전류의 흐름을 방해한다. ======직렬연결====== ======병렬연결====== =====축전기===== 서로 떨어진 두 도체(극판)으로 이루어져 있다. 전압을 가하면 전하를 축적할 수 있다. 콘덴서라고도 한다. ======전기 용량====== 축전기가 저장하는 전하량은 양 극판의 퍼텐셜차에 비례한다. ======평행판...) |
잔글편집 요약 없음 |
||
| (사용자 3명의 중간 판 11개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
[[분류: | [[분류:공학]][[분류:전자기학]] | ||
=저항= | |||
전류의 흐름을 방해한다. | 전류의 흐름을 방해한다. | ||
==직렬연결== | |||
===== | 저항을 직렬로 연결할 때 그 등가저항은 각각의 저항을 더한 것과 같다. | ||
<math> | |||
R = {R}_{1} + {R}_{2} + {R}_{3} | |||
</math> | |||
==병렬연결== | |||
저항을 병렬로 연결할 때 등가저항의 계산은 다음과 같다. | |||
<math> | |||
\frac{1}{R} = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \frac{1}{{R}_{3}} | |||
</math> | |||
=축전기= | |||
서로 떨어진 두 도체(극판)으로 이루어져 있다. | 서로 떨어진 두 도체(극판)으로 이루어져 있다. | ||
전압을 가하면 전하를 축적할 수 있다. | 전압을 가하면 전하를 축적할 수 있다. | ||
콘덴서라고도 한다. | 콘덴서라고도 한다. | ||
==전기 용량== | |||
축전기가 저장하는 | 축전기가 저장하는 전하량(Q)은 양 극판의 퍼텐셜차(V)에 비례한다. | ||
= | <math> | ||
Q = CV | |||
</math> | |||
이 때 비례상수 C를 전기 용량(혹은 정전 용량) 이라고 하며 | |||
단위는 [F], '패럿'으로 읽는다. | |||
==평행판 축전기의 전기 용량== | |||
양 극판을 평행하게 배치한 축전기를 평행판 축전기라고 한다. | |||
평행판 축전기의 전기 용량은 양 극판의 면적(S)에 비례하고 극판사이의 거리(d)에 반비례한다. | |||
<math> | |||
C \propto \frac{S}{d} | |||
</math> | |||
==직렬연결== | |||
축전기를 직렬로 연결하면 등가 전기용량은 마치 (평행판)축전기의 양 극판 사이의 거리가 멀어진 것과 같은 효과가 있다. | |||
<math> | |||
\frac{1}{C} = \frac{1}{{C}_{1}} + \frac{1}{{C}_{2}} + \frac{1}{{C}_{3}} | |||
</math> | |||
==병렬연결== | |||
축전기를 병렬로 연결하면 등가 전기용량은 마치 (평행판)축전기의 양 극판의 면적이 증가한 것과 같은 효과가 있다. | |||
<math> | |||
C = {C}_{1} + {C}_{2} + {C}_{3} | |||
</math> | |||
==용량성 리액턴스== | |||
<math display=block> | |||
{X}_{C} = \frac{1}{wC} = \frac{1}{2\pi f C} | |||
</math> | |||
==전기적 성질== | |||
# 직류는 딱히 통하지 않는다. | # 직류는 딱히 통하지 않는다. | ||
직류 걸어 봤자 적당히 충전되고 끝이다. | 직류 걸어 봤자 적당히 충전되고 끝이다. | ||
| 26번째 줄: | 63번째 줄: | ||
충전이 최대로 되었을 때 전류의 흐름을 상상하여 보자. | 충전이 최대로 되었을 때 전류의 흐름을 상상하여 보자. | ||
===== | =코일= | ||
===== | 도선을 일정한 방향으로 감아 만든 부품이다. | ||
==유도 리액턴스== | |||
자기장의 변화에 대한 이해 [[전기와 자기#렌츠의 법칙]] 가 반드시 선행되어야 하니 참고 바란다. | |||
코일은 도선을 모아둔 것이므로 전류가 흐르면 자기장이 발생한다. | |||
원기둥 막대에 도선을 감아 만든 코일을 생각하면 전류가 흘러 만들어진 자기장은 원기둥 막대의 내부를 통과한다. | |||
이 때 흐르는 전류가 직류가 아니라 교류라면, 회로의 내부를 통과하는 자기장 다발의 변화가 발생하는 것과 같다. | |||
이에 렌츠의 법칙에 의하여 유도기전력이 발생하여 코일은 마치 저항과 같이 작용하게 된다. | |||
이것을 유도 리액턴스라고 한다. | |||
<math display=block> | |||
{X}_{L} = wL = 2 \pi f L | |||
</math> | |||
=진공관= | |||
트랜지스터의 발명으로 사용 빈도가 줄어들고 있지만, 이런저런 이유로 여전히 사용중이기 때문에 알아두어야 한다. | |||
==열전자 방출== | |||
고체인 도체나 반도체를 가열할 때 전자가 고체 밖으로 튀어나오는 현상을 말한다. | |||
에디슨 효과라고 하기도 하며 진공관의 가장 기본적인 동작 원리이다. | |||
=반도체 부품= | |||
==다이오드== | |||
P형 반도체 하나와 N형 반도체 하나를 이용하여 전류가 한쪽 방향으로만 흐를 수 있도록 하는 부품이다. | |||
교류를 직류로 바꿀 때 사용할 수 있다. | |||
==== | ==트랜지스터== | ||
P형 반도체와 N형 반도체 중 어느 하나 사이에 다른 하나를 아주 얇게 끼워 둔 부품이다. | |||
전류의 증폭 등의 효과를 볼 수 있고, 경우에 따라 스위치와 같이 동작하기도 한다. | |||
[[파일:transister_pnp.png]] | |||
그림은 P형 반도체 사이에 N형 반도체를 둔 PNP형 트랜지스터이다. | |||
2022년 5월 23일 (월) 21:20 기준 최신판
저항
전류의 흐름을 방해한다.
직렬연결
저항을 직렬로 연결할 때 그 등가저항은 각각의 저항을 더한 것과 같다.
[math]\displaystyle{
R = {R}_{1} + {R}_{2} + {R}_{3}
}[/math]
병렬연결
저항을 병렬로 연결할 때 등가저항의 계산은 다음과 같다.
[math]\displaystyle{
\frac{1}{R} = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \frac{1}{{R}_{3}}
}[/math]
축전기
서로 떨어진 두 도체(극판)으로 이루어져 있다.
전압을 가하면 전하를 축적할 수 있다.
콘덴서라고도 한다.
전기 용량
축전기가 저장하는 전하량(Q)은 양 극판의 퍼텐셜차(V)에 비례한다.
[math]\displaystyle{
Q = CV
}[/math]
이 때 비례상수 C를 전기 용량(혹은 정전 용량) 이라고 하며
단위는 [F], '패럿'으로 읽는다.
평행판 축전기의 전기 용량
양 극판을 평행하게 배치한 축전기를 평행판 축전기라고 한다.
평행판 축전기의 전기 용량은 양 극판의 면적(S)에 비례하고 극판사이의 거리(d)에 반비례한다.
[math]\displaystyle{
C \propto \frac{S}{d}
}[/math]
직렬연결
축전기를 직렬로 연결하면 등가 전기용량은 마치 (평행판)축전기의 양 극판 사이의 거리가 멀어진 것과 같은 효과가 있다.
[math]\displaystyle{
\frac{1}{C} = \frac{1}{{C}_{1}} + \frac{1}{{C}_{2}} + \frac{1}{{C}_{3}}
}[/math]
병렬연결
축전기를 병렬로 연결하면 등가 전기용량은 마치 (평행판)축전기의 양 극판의 면적이 증가한 것과 같은 효과가 있다.
[math]\displaystyle{
C = {C}_{1} + {C}_{2} + {C}_{3}
}[/math]
용량성 리액턴스
[math]\displaystyle{
{X}_{C} = \frac{1}{wC} = \frac{1}{2\pi f C}
}[/math]
전기적 성질
- 직류는 딱히 통하지 않는다.
- 직류 걸어 봤자 적당히 충전되고 끝이다.
- 교류의 경우, 주파수가 높을 수록 전류가 잘 통한다.
- 충전과 방전이 빠르게 이루어지는것으로 생각하면 편하다.
- 교류의 경우, 전류의 위상은 전압의 위상보다 90도 빠르다.
- 충전이 최대로 되었을 때 전류의 흐름을 상상하여 보자.
코일
도선을 일정한 방향으로 감아 만든 부품이다.
유도 리액턴스
자기장의 변화에 대한 이해 전기와 자기#렌츠의 법칙 가 반드시 선행되어야 하니 참고 바란다.
코일은 도선을 모아둔 것이므로 전류가 흐르면 자기장이 발생한다.
원기둥 막대에 도선을 감아 만든 코일을 생각하면 전류가 흘러 만들어진 자기장은 원기둥 막대의 내부를 통과한다.
이 때 흐르는 전류가 직류가 아니라 교류라면, 회로의 내부를 통과하는 자기장 다발의 변화가 발생하는 것과 같다.
이에 렌츠의 법칙에 의하여 유도기전력이 발생하여 코일은 마치 저항과 같이 작용하게 된다.
이것을 유도 리액턴스라고 한다.
[math]\displaystyle{
{X}_{L} = wL = 2 \pi f L
}[/math]
진공관
트랜지스터의 발명으로 사용 빈도가 줄어들고 있지만, 이런저런 이유로 여전히 사용중이기 때문에 알아두어야 한다.
열전자 방출
고체인 도체나 반도체를 가열할 때 전자가 고체 밖으로 튀어나오는 현상을 말한다.
에디슨 효과라고 하기도 하며 진공관의 가장 기본적인 동작 원리이다.
반도체 부품
다이오드
P형 반도체 하나와 N형 반도체 하나를 이용하여 전류가 한쪽 방향으로만 흐를 수 있도록 하는 부품이다.
교류를 직류로 바꿀 때 사용할 수 있다.
트랜지스터
P형 반도체와 N형 반도체 중 어느 하나 사이에 다른 하나를 아주 얇게 끼워 둔 부품이다.
전류의 증폭 등의 효과를 볼 수 있고, 경우에 따라 스위치와 같이 동작하기도 한다.
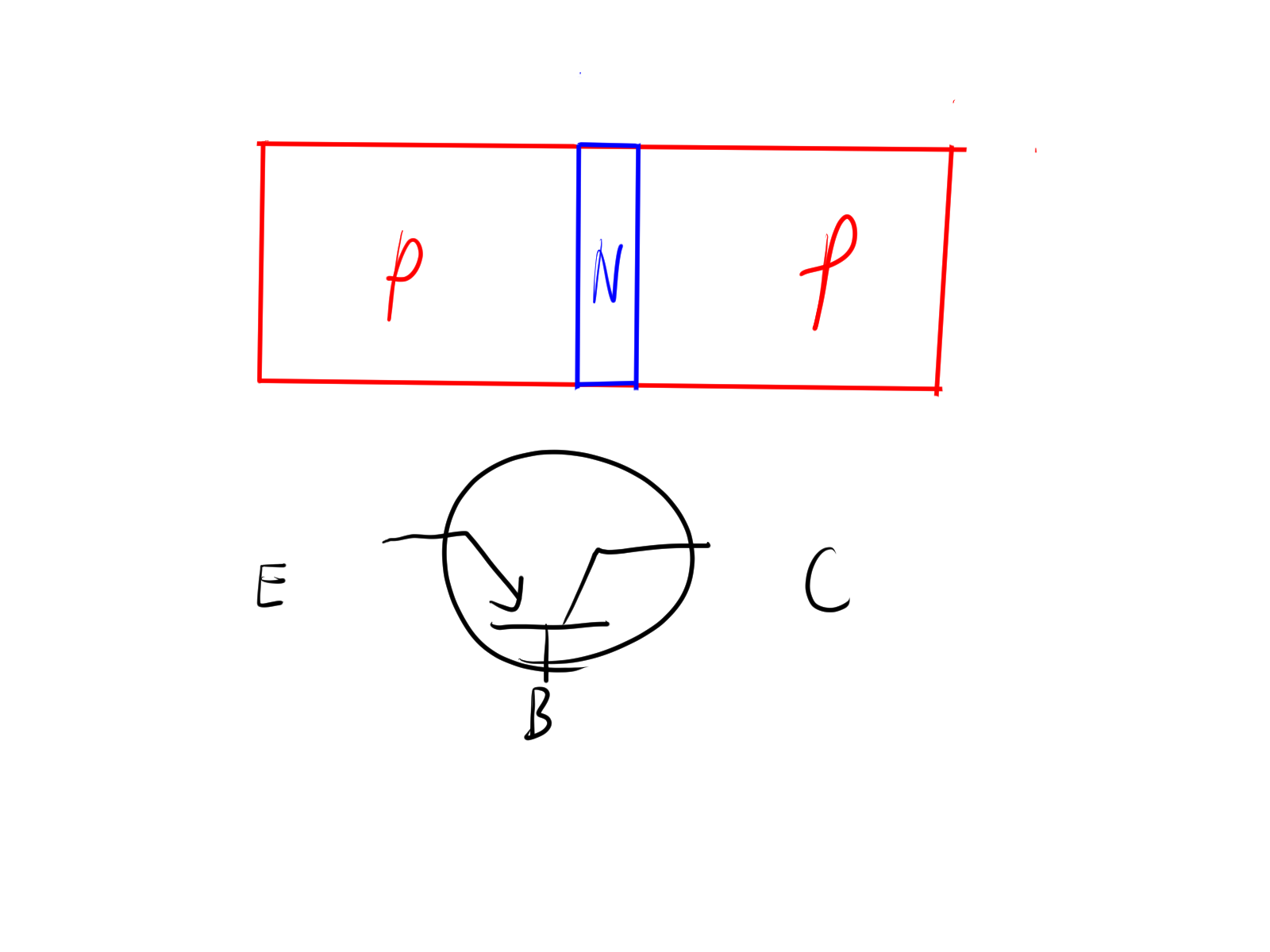
그림은 P형 반도체 사이에 N형 반도체를 둔 PNP형 트랜지스터이다.